Phần lớn tất cả mọi người đều biết tới quy luật một phần ba, đơn giản là bạn sẽ chia khung hình của mình theo cả chìa dọc và ngang thành 3 phần bằng nhau. Kết quả khung hình của bạn sẽ được chia làm thành 9 phần bằng nhau như hình bên dưới. Khi đó, thay vì đưa đối tượng vào chính giữa khung hình như nhiều người vẫn làm, bạn sẽ đưa đối tượng vào gần 4 giao điểm như trong ảnh. Điều này giúp bức ảnh trong tự nhiên hơn nhiều.

Các đường kẻ chia khung hình thành 9 phần bằng nhau. (Ảnh: Photographylife)
Khi chụp ảnh, bạn hãy thử tìm xem đâu là yếu tố quan trọng nhất, từ đó đưa đối tượng và gần 1 trong 4 giao điểm gần đường kẻ hoặc giao điểm càng gần càng tốt. Tất nhiên bạn sẽ cần điều chỉnh đối tượng tùy vào tình huống chứ không nhất thiết phải đưa chính giữa giao điểm hay trùng với đường kẻ. Dưới đây là một số ví dụ điển hình:




Một số ví dụ về quy tắc một phần ba. (Ảnh: creativemarket)
Như vậy bạn đã có thể hình dung rõ ràng hơn về quy tắc một phần ba phải không? Và như chúng ta đều đã biết, từ bao đời nay, quy luật một phần ba vẫn đang được tất cả mọi người sử dụng, từ những nhiếp ảnh gia chuyên nghiệp đến những người mới tập chụp ảnh.
Quy tắc một phần ba và tỉ lệ vàng
Chắc hẳn bạn cũng biết tới tỉ lệ, một khái niệm rất nổi tiếng. Tỉ lệ vàng có giá trị 1.618:1 và chính là kết quả xấp xỉ của phép toán ½ (1 + √ 5 ). Rất nhiều người đã cho rằng quy tắc một phần ba là sự giản lược của tỉ lệ vàng, đó là lý do vì sao tỉ lệ vàng “hoạt động”. Thế nhưng, hãy nhìn vào hình vẽ bên dưới, trong đó tỉ lệ vàng được biểu diễn bởi đường màu xanh, quy tắc một phần 3 là đường màu đỏ, bạn sẽ thấy khoảng cách giữa 2 đường là khá xa nhau.
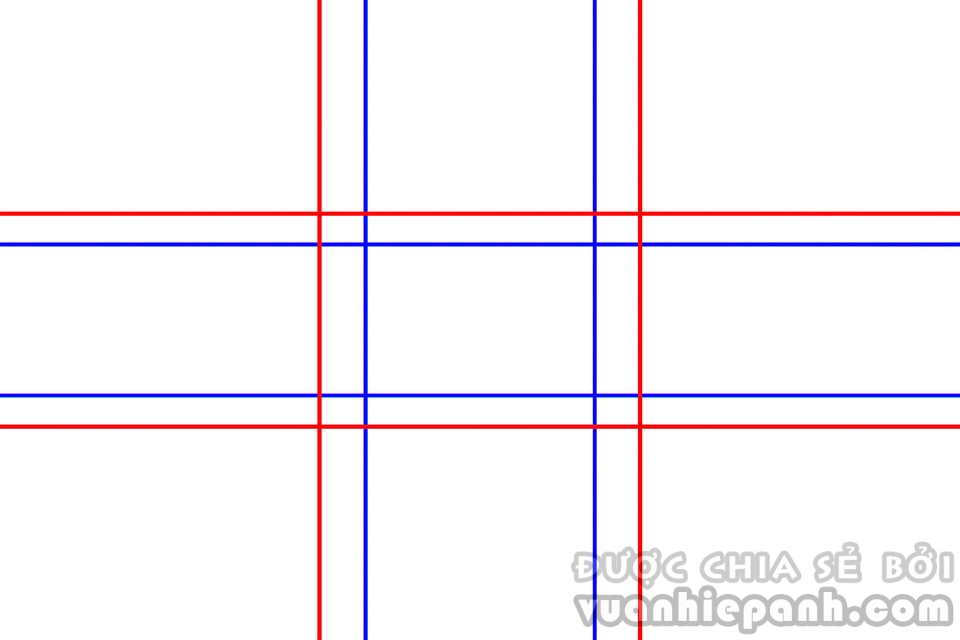
Kỳ thực, tỉ lệ vàng không có nhiều ý nghĩa trong thực tế. (Ảnh: Photographylife)
Kỳ thực, tỉ lệ vàng là một công thức thú vị trong toán học, nhưng trong quy tắc một phần ba hay trong thực tế, đó là hai vấn đề hoàn toàn khác nhau. Ví dụ điển hình có thể kể tới Đền Parthenon nổi tiếng. Không có bất cứ chi tiết nào trong ngôi đền Parthenon được thiết kế theo tỉ lệ vàng, các cột và dầm mái tạo thành các hình chữ nhật theo tỉ lệ 9:4 tức là xấp xỉ 2.25, cách rất xa so với tỉ lệ vàng là 1.618. Hoặc bạn có thể nhìn vào khung hình được tô màu đỏ phía trên, tỉ lệ giữa 2 cạnh là 1.71 khá gần với 1.618, có vẻ rất gần với tỉ lệ 1.71. Thế nhưng những người Hi Lạp cổ là những kiến trúc sư cực kỳ tài ba, nếu họ muốn ngôi đền Parthenon xây dựng dựa trên tỉ lệ vàng, họ thừa khả năng để xây dựng ngôi đền theo ý mình.

Đền Parthenon không được xây dựng theo tỉ lệ vàng.(Ảnh: Photographylife)
Giáo sư đại học Stanford giảng về tỉ lệ vàng trong lý thuyết và thực tế. Video cũng nói về đền Parthenon như vừa đề cập ở trên.
Khi nhắc đến tỉ lệ vàng bạn thường thấy tỉ lệ này biểu diễn dưới dạng đường xoắn ốc, nhưng công bằng mà nói những vật được biểu diễn dưới dạng đường xoắn ốc đều rất đẹp khiến mọi người thường nhầm tưởng tỉ lệ vàng là đặc biệt. Trong 4 đường xoắn ốc bên dưới, liệu bạn có thể chỉ ra đâu là đường xoắn ốc theo tỉ lệ vàng?
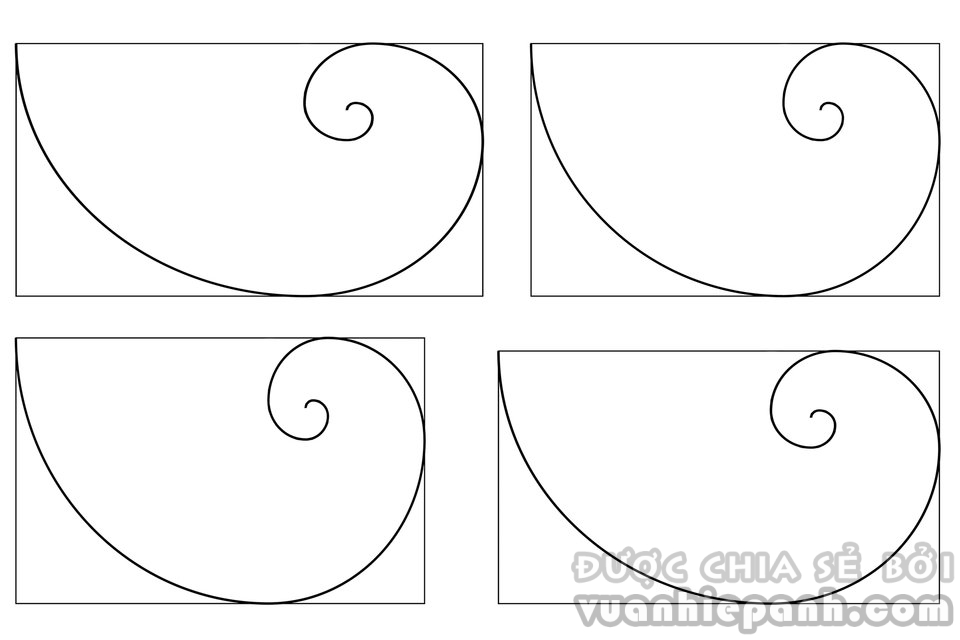
Đố bạn hình nào được biểu diễn bởi tỉ lệ vàng? (Ảnh: Photographylife)

Công bằng mà nói những vật có hình dạng xoắn ốc đều rất "hút" mắt. (Ảnh: Hoài Nam)
Vậy vì sao quy tắc một phần ba lại có thể “hoạt động”?
Cả nhiếp ảnh gia và các họa sĩ đều áp dụng quy tắc một phần ba khi chụp ảnh hay vẽ tranh. Đơn giản vì qua thời gian, quy tắc này đã chứng minh được sự hiệu quả. Có một cách đơn giản để lý giải vì sao quy tắc này “hoạt động”: khi bạn đạt chủ thể của mình nằm chính giữa khung hình, khoảng cách đồng đều từ 4 phía tới chủ thể cân bằng khiến bức ảnh của bạn “bất động”. Vì vậy, khi chúng ta đặt chủ thể ra xa phía góc ảnh, mắt chúng ta sẽ hướng theo đường đi chủ thể mang đến cảm giác “sống động” hơn rất nhiều so với việc để chủ thể ở chính giữa.

Bức ảnh tuân theo quy tắc một phần ba giúp ảnh như đang "chuyển động". (Ảnh: internet)
Quy tắc một phần ba “mở rộng”

Nhìn vào bức ảnh này, có vẻ bố cục đã được tuân theo quy tắc một phần ba. (Ảnh: Photographylife)

Không, mắt của chủ thể không nằm ở giao điểm nhưng bức ảnh trông vẫn hoàn toàn ổn phải không? (Ảnh: Photographylife)
Trong thực tế, bạn sẽ gặp rất nhiều bức ảnh tương tự như bức ảnh phía trên. Vì vậy, không nhất thiết phải tuân theo một cách chính xác hoàn toàn. Chúng ta có thể tăng độ rộng của các đường kẻ như trong hình bên dưới. Lúc này, bạn chỉ cần đặt chủ thể vào khu vực giao điểm màu đỏ như trong hình bên dưới và ảnh của bạn vẫn hoàn toàn dự trên quy tắc một phần ba đấy chứ.

Quy tắc một phần ba "mở rộng". (Ảnh: Photographylife)
Ảnh phải luôn chụp theo quy tắc một phần ba?
Chắc chắn là không, không phải lúc nào bạn cũng phải tuân theo quy tắc một phần ba cho bức ảnh của mình. Nhiếp ảnh cần sự sáng tạo và nếu bạn cảm thấy bố cục khác đẹp hơn, đừng ngại ngùng phá vỡ quy tắc.
Ví dụ trong bức ảnh chụp cặp đôi bên dưới, bạn có thể dễ dàng nhận thấy bức ảnh nào không hề tuân theo quy tắc một phần ba. Thế nhưng độ sâu trường ảnh mỏng đã giúp cặp đôi hoàn toàn nổi bật trên bức ảnh. Đây là một ví dụ điển hình về sự sáng tạo trong chụp ảnh. Bạn hoàn toàn có thể chụp chủ thể ở chính giữa bức ảnh khi chụp chân dung.

Một ví dụ cơ bản về việc phá vỡ quy tắc một phần ba. (Ảnh: internet)
Quy tắc một phần ba là công cụ cực kỳ hữu ích cho những người mới bắt đầu chụp ảnh. Quy tắc này giúp chúng ta hiểu được tác dụng của việc đặt chủ thể về phía góc ảnh thay vì khu vực trung tâm như họ vẫn làm trước đó. Qua thời gian, khi đã hiểu rõ hơn về bố cục, các nhiếp ảnh gia sẽ không chỉ lệ thuộc vào quy tắc đó.


Ý kiến bạn đọc