- Đối tượng chụp không định vị được
Đường thẳng không định hướng được
Các ngoại lệ
Từ bỏ quy tắc
- Tỷ Lệ Vàng
Fibornacci
Quy tắc 1/3 phỏng theo Fibonacci là rất dở hơi
Quy tắc 1/2 có khi phổ biến hơn 1/3 trong thiên nhiên
- Kết luận
Không nên lấy quy tắc 1/3 làm mặc định
Mạnh dạn sáng tạo, nếu không muốn ảnh của mình na ná giống ảnh ai đó.
1. Quy tắc một phần ba là gì?
Hầu hết những ai đọc đến đây đều đã biết về quy tắc một phần ba. Đơn giản đó chỉ là một mạng lưới những đường thẳng chia khung hình thành chín phần bằng nhau. Quy tắc một phần ba từng được nhiều người, kể cả một số nhiếp ảnh gia chuyên nghiệp chọn làm thành quy tắc hướng dẫn cho việc sắp xếp một bố cục thành công – nó gợi ý người chụp đặt các đối tượng được chọn nằm trên một trong bốn đường thẳng (màu xanh), hoặc, lý tưởng hơn, nằm tại một trong bốn điểm giao cắt (màu vàng) như hình bên dưới:
![[IMG]](/uploads/news/ky-thuat-nhiep-anh/bo-cuc/duong-thang/bo-cuc-anh.png)
2. Đối tượng chụp không thể định vị theo quy tắc một phần ba
Với đối tượng nhỏ, rõ ràng: Nếu để ý, các bạn không khó để nhận thấy sự hiện diện của quy tắc một phần ba trong nhiều bức ảnh - đặc biệt là những bức ảnh có đối tượng tương đối nhỏ, đơn nhất và tách bạch rõ ràng so với các sự vật khác xuất hiện trong ảnh. Chẳng hạn bạn chụp một con chim đơn độc trên nóc nhà, đang bay, một con người trên biển rộng, hay cái xe đi trên đường vắng... thì đúng là quá dễ để nói rằng Oh! con chim, con người, hay cái xe, cục đá... có nằm ở điểm giao cắt / điểm mạnh theo quy tắc một phần ba hay không.
Ví dụ:
Lấy ví dụ chú nai là khá lớn, nhưng là chủ thể rõ ràng, tách bạch so với cảnh trí phụ hoạ xung quanh. Ta có thể đặt điểm nhất là vùng đầu, mõm, mắt tai con nai vào điểm giao cắt 1/3 theo đúng quy tắc.
Lấy ví dụ chú nai là khá lớn, nhưng là chủ thể rõ ràng, tách bạch so với cảnh trí phụ hoạ xung quanh. Ta có thể đặt điểm nhất là vùng đầu, mõm, mắt tai con nai vào điểm giao cắt 1/3 theo đúng quy tắc.

Ảnh tuanlionsg - Nikon D8100
Nhưng:
Với đối tượng quá lớn: Với những đối tượng quá lớn, không thể trùng khít với đường giao cắt được, ngay cả khi nó vắt ngang trong môt ô 1/3 đúng theo quy tắc. Thường thấy phổ biến với những ảnh phong cảnh, kiến trúc... mà người chụp vốn chỉ quan tâm đến những đối tượng rộng lớn, ranh giới các vật thể không thể xác định rõ ràng, nhưng chắc chắn nó vẫn hiệu quả với nhiều thể loại.
Ví dụ:
Hãy nhìn bức ảnh bên dưới, đối tượng là ngôi thánh đường rất lớn, bạn sẽ đặt nó vào điểm giao cắt thế nào?
Hãy nhìn bức ảnh bên dưới, đối tượng là ngôi thánh đường rất lớn, bạn sẽ đặt nó vào điểm giao cắt thế nào?

Ảnh tuanlionsg - EOS 6D AIS 15mm f/3.5
Bây giờ hãy nhìn vào bức ảnh với mạng lưới đường giao trong quy tắc một phần ba để so sánh :

Như bạn có thể thấy, chiều dài ngôi thánh đường thực sự giao cắt với đường cắt ngang thứ 2. Nhưng nó còn trải rộng đáng kể cả hai phía trên tháp chuống và phía trên lẫn dưới đường cắt số 2 ấy – thực ra, đường cắt ngang thứ hai cũng giao cắt ở nhiều điểm như bất cứ đường cắt ngang nào từ phần cung thánh nhà thờ đến 2/3 khung ảnh. Đối tượng chiếm một góc toàn bộ phần 1/3 của mạng lưới các ô đúng như kỹ thuật, nhưng sẽ là sai lầm khi nghĩ rằng bức ảnh này là một thí dụ về quy tắc một phần ba. Không thể nói một chỉnh thể nào của một toàn thể đối tượng (ngôi thánh đường) là chính hay phụ.
Với đối tượng là phối cảnh trườu tượng, có nhiều chủ thể: Điều gì xảy ra khi bạn chụp một cảnh trí trừu tượng hoặc có nhiều chủ thể ? Có thể sắp xếp bố cục của nó như một bức ảnh có sử dụng quy tắc một phần ba không? Mình nghĩ là không – nếu đối tượng của bạn không tương đối nhỏ và được xác định rõ, thì trước hết, gần như không thể nói được nó có phù hợp với quy tắc một phần ba hay không.

Ảnh tuanlionsg - Yashica 6x6 Film


Bạn có thể biện bạch cho rằng hai bức ảnh trên phù hợp với quy tắc một phần ba – chí ít, một thứ nào đó giao cắt với các đường 1/3 và 2/3. Nếu vậy, tất cả các thành tố của bức ảnh này sẽ đều giao cắt với bất kỳ (thậm chí là vô số) đường thẳng nào được kẽ dọc theo khung hình, nhưng đối tượng chính (đoàn người đang băng qua đồi cát) lại hoàn toàn không phù hợp với quy tắc một phần ba. Đây cũng không phải là một bức ảnh quá hiếm gặp – hầu như mỗi lần bạn chụp một bức ảnh góc rộng nào đó, thì quy tắc một phần ba có thể tự động được thực hiện để phù hợp với cảnh chụp.
3. Mạng lưới đường thẳng không rõ ràng
Không khó để ép một bức ảnh chụp phù hợp theo quy tắc một phần ba, với điều kiện chủ thể phải không quá lớn, đơn nhất, tách bạch rõ ràng so với phối cảnh chung. Hầu như tất cả, bạn chỉ cần tập luyện, là có thể ép chủ đề của mình tuân đúng quy tắc.
Vậy, sẽ ra sao khi đối tượng dễ xác định, nhưng nằm ngoài các điểm giao, các đường thẳng phân chia phần ba một khoảng nào đó?
 Ảnh tuanlionsg - Nikon D3 AIS 105mm f/2.8
Ảnh tuanlionsg - Nikon D3 AIS 105mm f/2.8Mắt con chuồn chuồn trong ảnh chắc chắn trông có vẻ phù hợp với quy tắc một phần ba. Nhưng khi vạch các đường giao cắt 1/3 thì sẽ thế nào ?

Vâng, mắt con chuồn chuồn có nằm hơi lệch ra ngoài điểm giao cắt 1/3 một chút. Và chúng ta sẽ nói rằng Oh, có gì là ghê gớm đâu, phải không nào ? Bức ảnh này hầu như hoàn toàn tuân thủ quy tắc một phần ba.
Như vậy, thì “quy tắc một phần ba” trở thành “quy tắc về những gì trông na ná như một phần ba”. Như vậy, có một chuyển biến dần dần – càng đặt đối tượng chụp của bạn cách xa các mốc đánh dấu 1/3 bao nhiêu, thì rõ ràng bức ảnh của bạn càng ít phù hợp với quy tắc bấy nhiêu. Nếu thế, ta dựa vào tính chất uyển chuyển ấy, quy tắc một phần ba được sửa đổi: thay vì đặt đối tượng chụp vào điểm giao của các đường thẳng thì khuyên đặt đối tượng chụp của mình vào vùng màu (diện tích rộng hơn điểm giao):

Nhưng như thế thì hoàn toàn không đúng, bởi vì theo quy tắc một phần ba, hầu hết mọi người đều sẽ khuyên không nên đặt đối tượng chính nằm sát mép bức ảnh, sát rìa khung ảnh. Tức là chủ thể chính phải nằm gần vùng trung tâm hơn, nên ta lại phải sửa đổi mạng lưới đường thẳng cho nó trông như thế này mới đúng :

Giờ thì chúng ta có quy tắc những điểm phình lên. Nếu đặt đối tượng nằm tương đối trong khu vực màu xanh, bạn sẽ dễ dàng thuyết phục những người chụp ảnh khác tin rằng bức ảnh của bạn tuân thủ theo quy tắc một phần ba. Một số giám khảo hoặc vô số người xem sẽ chấm đó là khung ảnh thành công!
4. Có ngoại lệ
Mỗi bài học về quy tắc một phần ba mà mình thường được nghe các thầy dạy, đều có kết thúc như sau: “Bên cạnh đó, cũng có những ngoại lệ đối với quy tắc. Đôi khi, bạn muốn sắp xếp bố cục bức ảnh của mình không theo quy tắc một phần ba. Việc đó chả sao cả! Là một người chụp ảnh, bạn có quyền quyết định về diện mạo của bức ảnh bạn chụp. Đừng sợ phá vỡ quy tắc khi, theo một cách khác, bức ảnh bạn chụp vẫn đẹp hơn.”
Vậy mới thấy quy tắc một phần ba không rõ ràng về các điểm phình mỗi lúc mỗi trở nên lờ mờ hơn: “Nói chung, bạn hãy đặt đối tượng vào bên trong ô màu xanh ở trên. Nhưng nếu bức ảnh trông đẹp hơn so với các cách làm khác, thì đừng ngại từ bỏ quy tắc”. Có thể điểm nổi trội của quy tắc một phần ba là khuyên bạn đặt đối tượng ở bất cứ chỗ nào mà bạn muốn trên khung hình miễn bạn cảm thấy hợp với ý muốn diễn tả. Nếu đúng như vậy, mình hoàn toàn đồng ý.
Thêm một ý là điều mà Henri Cartier-Bresson ngày trước - thời máy phim - không muốn nhìn thấy thì bây giờ đã xảy ra. Đó là ngày mà tất cả các máy ảnh đều gợi ý hiển thị khung bố cục một phần ba/ tỷ lệ vàng ở kính ngắm máy thiết bị ghi hình, hoặc trên tấm kính mờ lấy nét hoặc màn hình live-view.

Ảnh tuanlionsg - EOS 6D
5. Từ bỏ quy tắc
Một số người chụp ảnh ủng hộ quy tắc một phần ba bằng cách nói nó là công cụ học hỏi hữu ích dành cho người mới bắt đầu – theo thời gian, những người chụp ảnh có kinh nghiệm tay nghề cao đều không còn dựa vào nó để sắp xếp bố cục cho các bức ảnh của họ nữa. Gợi ý của mình ở đây là nghiên cứu quy tắc một phần ba một cách nghiêm túc, sau đó là từ bỏ nó.

Ảnh tuanlionsg
Trong số tất cả những biện luận về quy tắc một phần ba, mình đồng ý với lời biện luận ở trên đây. Mình tin rằng, đến một lúc nào đó, quy tắc một phần ba trở thành một phương cách giúp cho những người mới bắt đầu chụp ảnh nhìn dễ dàng thấy được sức mạnh của một bố cục có đối tượng chụp nằm xa trung tâm khung hình. Dĩ nhiên, đa số những người mới bắt đầu chụp ảnh đều lên khung cho các bức ảnh của họ với những bố cục hoàn toàn tập trung vào trung tâm – biết đâu quy tắc một phần ba giúp họ nhận ra các đối tượng lệch tâm cũng có thể rất đẹp.

Ảnh tuanlionsg
Nhưng nếu muốn nói với những người mới bắt đầu chụp ảnh thấy rằng những bố cục có đối tượng lệch tâm có thể trông rất đẹp, vậy tại sao không nói thẳng luôn như vậy đi? Giả như quy tắc một phần ba là một trung gian giữa những người mới bắt đầu và kiến thưc của họ về các bố cục lệch tâm, thì mình chẳng thấy có lý do gì mà quy tắc đó lại chiếm vị trí ưu tiên khi bình ảnh cả. Nếu như với những người mới bắt đầu chụp ảnh có suy nghĩ một cách sáng tạo, thì phương pháp nào sau đây hiệu quả hơn: Chỉ cho họ chụp những bức ảnh theo quy tắc một phần ba, hay chỉ cho họ chụp những bức ảnh có đối tượng nằm lệch tâm? Có thể cả hai đều có hiệu quả như nhau, nhưng phương pháp sau còn lâu mới bị hạn chế như phương pháp theo quy tắc.
Vì thế, rất nhiều người bắt đầu học chụp, chỉ xem qua cho biết quy tắc một phần ba, và vượt qua nó để sáng tạo những kết cấu các thành phần trong ảnh sáng tạo, diễn tả mạnh mẽ hơn ý đồ và lượng thông tin mà họ muốn chuyển tải qua khung ảnh hơn.

Ảnh tuanlionsg - Zenfone 5
6. Tỉ Lệ Vàng Fibornacci
Chúng ta biết, quy tắc một phần ba truyền thống cũng không phải tự sinh ra, mà người ta nói nó khởi nguồn từ tỷ lệ vàng nổi tiếng – tỉ lệ vàng. Tỉ lệ vàng 1.618 : 1, là một số xấp xỉ với biểu thức toán sau đây: ½ (1 + √ 5 )
Con số được coi trọng vì dựa theo dãy số Fibonacci mà trong đó mỗi số đều là tổng của hai số đi liền trước nó : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, và cứ tiếp tục như thế. Nếu chia một số trong dãy Fibonacci với số đi trước nó, thì bạn đang tiếp cận với tỉ lệ vàng. Ví dụ, 89/55 làm tròn thành 1.618.
Chúng ta thường nghe người ta nói rằng quy tắc một phần ba được rút gọn thành tỉ lệ vàng, đó là lý do tại sao nó “hiệu quả”. Về vấn đề này, chúng ta có 2 nhận xét:
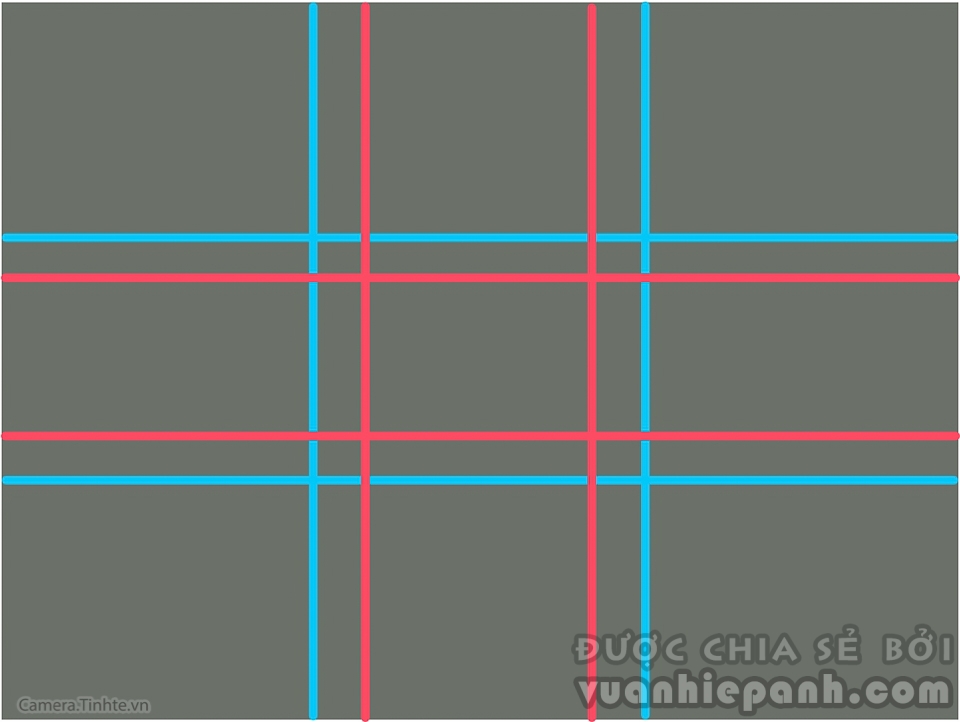
1/ Nếu quy tắc một phần ba là một phỏng theo tỉ lệ vàng, thì đúng là nó rất dở. Hãy xem các mạng lưới đường thẳng bên dưới (quy tắc một phần ba màu xanh, tỷ lệ vàng fibornacci màu đỏ). Nếu quy tắc một phần ba được nhiều người muốn làm cho hoàn toàn trở thành tỉ lệ vàng viễn tưởng ấy, thì tại sao nó không được dạy luôn như vậy đi – và tại sao những đường gióng trong máy ảnh dùng vào việc sắp xếp bố cục lại chia khung hình thành các phần ba, thay vì thành tỉ lệ vàng? Chưa kể đến mạng lưới các ô như thế làm cho các điểm giao cắt phình to ra và trở nên mù mờ hơn.
2/ Dẫu sao thì nó cũng chẳng có ý nghĩa gì. Điểm này có thể gây tranh luận và phản ứng của nhiều người. Đó là có phải hình chữ nhật/giá trị trung bình/tỉ lệ vàng luôn xuất hiện trong tự nhiên không? Và nếu người Hi lạp đã từng dùng con số ấy làm cơ sở để xây dựng đền Parthenon, thì hẳn là nó phải có một giá trị thực chất nào đó chứ?
Hãy xem xét hai công bố phổ biến về tỉ lệ vàng : xuất hiện trong những đường xoắn ốc trong dãi ngân hà và trên những vỏ ốc anh vũ. Anh em xem ảnh dưới được mượn từ Logarithmic Spiral:


Ảnh Logarithmic Spiral
Mặc dầu cả hai mẫu đều điển hình đi theo đường xoắn logarit, nhưng tỉ lệ vàng chỉ là một trường hợp rất cá biệt của logarit mở rộng – hiếm khi các góc đặc trưng trong các dãy thiên hà hoặc vỏ ốc trùng với các góc của đường xoắn vàng, một phần bởi vì các đường xoắn ốc trong dãy thiên hà và trên vỏ ốc tự chúng vốn đã khác nhau. Nếu các đường xoắn ốc các dãy thiên hà không có các góc như nhau, thì làm thế nào chúng có thể trở thành khuôn mẫu cho đường xoắn vàng được ? Các chi tiết quá đặc thù anh em có thể đọc thêm thông tin trên trang Logarithmic Spiral Wikipedia.
Đồng ý, tỉ lệ vàng là một con số toán học thú vị, nhưng không vì thế mà trở thành lý do cố định đóng khung để trở thành chuẩn mực đối với nhận thức của con người về vẻ đẹp thiên nhiên – đặc biệt là khi thấy nó không thường xuyên xuất hiện trong thế giới tự nhiên.
Nhiều tài liệu lấy đền Parthenon để thể hiện tỉ lệ vàng thì sao. Cứ việc đặt chồng hầu hết các hình chữ nhật lên đền Parthenon rồi tuyên bố nó phù hợp một cách kỳ diệu với tỉ lệ mà bạn muốn – có đủ những “điểm bắt đầu” dọc theo đên Parthenon để làm như vậy – nhưng hình chữ nhật rõ ràng nhất trong đền Parthenon (như hình dưới đây) lại có tỉ lệ chính xác là 9 : 4, hoặc 2.25. Điều này khác xa với tỉ lệ vàng 1.618.

Ảnh Wikimedia
Đây là hình chữ nhật mà rất nhiều người cho rằng phù hợp với tỉ lệ vàng. Nếu hình chữ nhật màu đỏ trong bức ảnh trên đây được mở rộng trùm lên cả đỉnh của mặt tiền, cũng như bậc cấp thấp nhất (sau đó mở rộng ra đến mép ngoài của mặt tiền), thì tỉ lệ của nó là khoảng 1.71. Vâng, con số này gần với con số 1.618, nhưng người Hi lạp cổ đại là một tập thể người thông minh – giả như họ muốn đền Parthenon thể hiện tỉ lệ vàng, hẳn là họ đã xây một hình chữ nhật “hoàn toàn” chính xác rồi. Đa số các biểu đồ bạn xem trên mạng trực tuyến đều sử dụng những đường thẳng đủ đậm và quãng cách đủ lớn để điều chỉnh lại độ chênh lệch 5% kia, nhưng sự khác biệt còn lớn hơn cả trong thế giới thực tế - đền Parthenon rộng gần 70 mét.
Tuy nhiên, cũng đáng để nhắc lại rằng tỉ lệ vàng có xuất hiện trong một vài khía cạnh của thế giới tự nhiên – hoặc, chí ít, dãy số Fibonacci có xuất hiện. Ví dụ, khi những chiếc lá xoắn quanh một thân cây, chúng thường xoắn theo một phần nhỏ vòng tròn mà có thể được biểu diễn bằng hai con số Fibonacci – như 1/2 hoặc 5/13. Nhưng cả khi như vậy, đường xoắn đó cũng không giống như tỉ lệ vàng – nó chỉ sử dụng hai con số trong cùng một chuỗi.

Ảnh gilkalai - formula fibornacci
Những đường xoắn, nói chung, đều đẹp, làm cho dễ tin rằng đường xoắn vàng là đặc biệt – chẳng nghi ngờ gì, nó trông rất tuyệt. Nhưng trong bốn biểu đồ dưới đây, bạn có thể nói đâu là đường xoắn vàng được không? Nếu được, nó có thật sự đẹp hơn các đường xoắn khác không ?
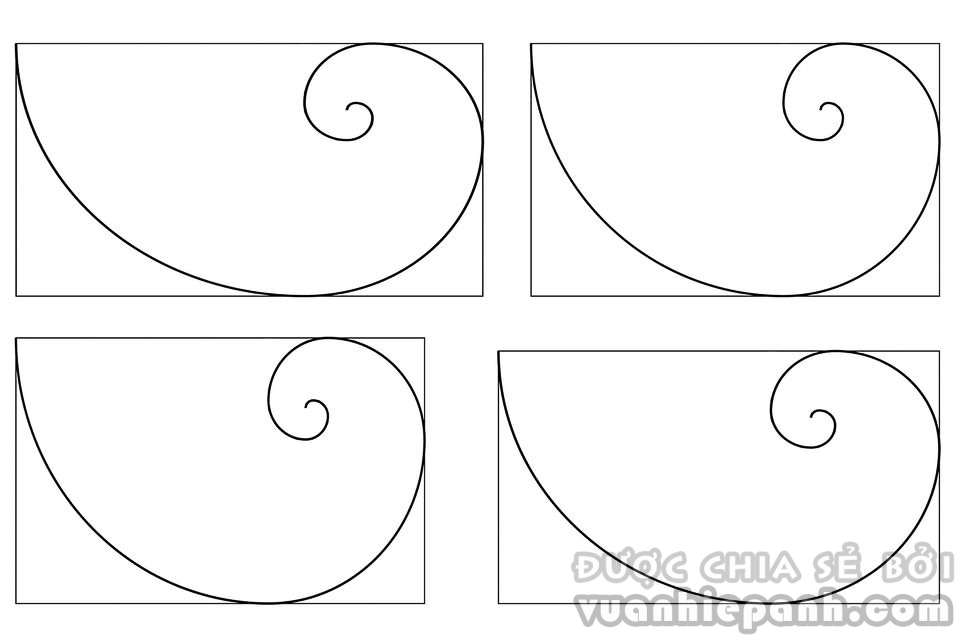
Điều trớ trêu là quy tắc một phần ba còn xa mới xuất hiện thường xuyên trong thiên nhiên hơn đường xoắn vàng – và chỉ có quy tắc một phần hai mới phổ biến hơn cả, chí ít là trong thế giới động vật. Điều này có nghĩa là tỉ lệ ½ đẹp hơn tỉ lệ, ví dụ, 17/23 chăng?
* Phần này có thể không đồng thuận với nhiều người. Nếu bạn cũng không đồng ý, mời bạn xem đoạn clip bàn về tỷ lệ vàng rất tỉ mỉ thấu đáo về tỷ lệ vàng, cuộc tranh luận về đền Panthenon:
7. Kết luận
Vâng, dĩ nhiên, toàn bộ bài viết này là một cái nhìn theo hướng khác quy tắc bất di dịch một phần ba. Những người chụp ảnh thuần thục đều hiểu rằng giá trị một bức ảnh chẳng liên quan gì đến việc nó khớp với một quy tắc một phần ba mang tính giáo điều. Cũng vậy, rất nhiều người đồng ý cho rằng phương pháp tốt nhất để sắp xếp bố cục của một bức ảnh thay đổi tùy theo cảnh chụp đặc thù cụ thể tuỳ bối cảnh xuất hiện trước ống kính.
Mối nguy hại nằm ở chỗ những người chụp ảnh cứ lấy quy tắc một phần ba đặt làm mặc định. Thói quen đó mở đường cho những cách sắp xếp bố cục luộm thuộm, khô cứng – đặt đối tượng ra bên cạnh điểm giao cả khi họ biết một bố cục ở vùng trung tâm có thể là tốt nhất, chẳng hạn vậy. Và ngay cả khi tất cả những người chụp ảnh đều biết quy tắc ấy có thể bị phá vỡ, nhưng lại không đưa điều ấy ra thực hành khi bấm máy.
Có thể quy tắc một phần ba giúp cho một người mới bắt đầu chụp ảnh thấy được tác dụng mạnh mẽ của việc lên khung lệch tâm. Bản thân mình ngày trước mới học chụp cũng thế. Nghe những lời phán như đinh đóng cột của những thầy dạy. Nhưng tkỳ thực quy tắc sẽ đánh mất gía trị của nó khi chính nó hạn chế cách xử lý sáng tạo của người chụp ảnh. Quy tắc một phần ba, buộc bạn hoặc đi theo nó, hoặc chủ ý phá vỡ nó – bởi nó hạn chế hoàn toàn sự sáng tạo của bạn.
Tâm lý những người mới học chụp ảnh, thật là tuyệt khi nghĩ rằng mình có thể cải thiện các bố cục ảnh thông qua một thủ thuật đơn giản như thế - quy tắc một phần ba, nhưng điều dễ dàng ấy lại chẳng bao giờ có tác dụng trong suốt chặng đường dài. Để vượt qua những cơ bản về sắp xếp bố cục, bạn tự giam hãm mình như thể chẳng có lựa chọn nào khác ngoài quy tắc dễ dàng ấy. Tại sao lại gây trở ngại cho sự tiến bộ bằng những quy tắc làm giảm đi sự sáng tạo như thế ?
Xin hãy cân nhắc kỹ điểm cuối cùng này : quy tắc một phần ba là cách tốt nhất chỉ để sắp xếp bố cục bức ảnh của bạn giống như của một ai đó. Nhìn vô số những bức ảnh, các cuộc triển lãm ảnh nghệ thuật, ngoài màu sắc hay sự vật khác nhau, còn lại nó cứ na ná một khung ảnh của ai đó mà mình đã từng xem đang ẩn trong vô thức vậy. Ngay cả khi quy tắc có những tính chất đặc biệt đi nữa, thì giá trị của sự sáng tạo bằng thị giác trong nhiếp ảnh là một sự tự do không thể bị đánh cắp bởi bất kỳ quy tắc nào.

Ảnh tuanlionsg - Galaxy Note5
8. Thực hành
Đến bài này, bạn thử tự hỏi, trước khi bấm nút chụp, rằng bạn muốn chủ thể chính mà bạn định chụp nằm ở vị trí nào trong phạm vi khung hình. Nó nằm ở trên cao hay dưới thấp, gần cạnh đứng hay cạnh ngang rất cao hay rất thấp, hay bạn muốn nó nằm giữa trung tâm ảnh?
Vị trí bạn đặt máy cũng có thể là một cách sẽ chọn hình dáng nào: thẳng, xiên, đứng, ngang hay bất thường? Hình nào làm xương sống cho bố cục chung để xếp các đối tượng vật thể bám theo cái sườn đó? Bức ảnh cuối cùng là vuông, dài, hẹp, hay rất hẹp, rất cao...? Quyết định của bạn là quyết định tỷ lệ khung hình, táo bạo hay quen thuộc, hình dáng, đường nét, mảng màu xuất hiện chủ ý hay ngẫu nhiên, hỗn độn hay trật tự là đều do sáng tạo và cảm nhận của bạn về sự hài hoà hiệu quả nhất mà bạn muốn ghi hình lại.
Ví dụ nhỏ:
Đặt máy góc rất thấp, nhìn đối tượng như qua vách đá:
Đặt máy góc rất thấp, nhìn đối tượng như qua vách đá:

Ảnh tuanlionsg - Galaxy S7
Đặt máy góc cao ngang tầm mắt, các vật thể xuất hiện nhiều hơn:

Ảnh tuanlionsg - Galaxy S7
Xin cảm ơn các bạn.


Ý kiến bạn đọc